Module 114 – Codage chiffrage

Compétence

Mettre en œuvre des systèmes de codification, de compression et de chiffrage.

Objectifs opérationnels

• Choisir et utiliser des procédures de compression appropriées d’archivage des informations. Démontrer quels sont les effets de la codification sur la transmission des données.
• Choisir et utiliser selon directives des procédures de compression pour la sauvegarde, la restauration et la transmission de données.
• Choisir et utiliser des procédures de chiffrage pour la sécurité des informations contre l´accès non autorisé en mémoires et sur des voies de transmission.
• Utiliser des procédures sûres de transfert de fichiers au moyen de procédures de chiffrage asymétriques et symétriques. Prendre en considération les aspects tels que clés publics/clés privées, les certificats, les protocoles et les normes.
• Évaluer les différentes technologies de chiffrage en ce qui concerne l’actualité, la distribution et la sécurité. Identifier les risques et proposer des technologies alternatives.

Voir le descriptif détaillé des objectifs du module…

• Support de cours eit du module 114…
• Support de cours de M. Butty

Table des matières

• Histoire
• Codage d’un fichier informatique
• Codage en télécommunication
  • Codage de source
  • Coder l’information
  • Code ASCII
  • Analogie biologique
  • Codage de Voie (canal)
• Redondance
• Compression de données
  • Compression non destructive de données
  • Compression destructive
  • Algorithme JPEG
  • Algorithme PNG
  • Principe de codage des couleurs d’un pixel
  • Steganographie
  • Compression de données Audio
  • Exercice de récapitulation
• Compression des fichiers déjà compressés
• Correction d’erreur
• Code correcteur de Hamming
• Conversion analogique numérique
  • Echantillonnage
  • Quantification
  • Modulation PCM
  • Ecouter le silence
• Codec
• Modulation

Tout le monde sait que les ordinateurs et les transmission informatiques sont basées sur un codage de l’information faites de 0 et de 1. Un code binaire. Mais quel est ce code ?

En fait il y a de nombreux codes possibles, et même plusieurs couches de codes différents imbriqués pour coder une information, pour la transmettre de façon adaptée au moyen de transmission et pour éviter, voir même corriger les erreurs.

Histoire

Nous sommes entouré de code, il suffit de regarder autour de toi, et je suis certain qu’il y a un code barre pas loin….

C’est une suite de barre de largeur différente qui code de l’information numérique.

Depuis des millénaires les humains codent de l’information.

C’est le cas des tablettes d’argile utilisées depuis au moins -3200 … Mais probablement avant…

Avant les tablettes, il y avait les calculi, des petits jetons d’argile permettant de faire de la comptabilité.

Code binaire

Le système de numération binaire « moderne » a été publié en 1703 par Gottfried Leibniz qui présente ainsi 25 ans de recherche sur ce sujet. Notamment inspirée par le Yi Jing chinois vieux de plusieurs millénaires.

010101010111

Exercice: essayez de compter en binaire sur les doigts (digital !)

On prend la main droite pour compter.
Le 0 c’est le doigt plié en bas.
Le 1 c’est le doigt levé.

Le pouce représente le premier digit, puis l’index, le second, le majeur le 3ème bit, l’annulaire le 4ème, etc….
On lit de droite à gauche, comme les chiffres indo-arabes habituel. Bit de poids faible à droite, bit de poids fort à gauche.

Hop… c’est parti…

Donc en numérique, on n’enregistre plus directement la forme de la variation d’une grandeur physique, mais on enregistre une suite de nombre qui représente cette variation physique.

Ainsi il est nécessaire de connaitre le code utilisé pour coder l’information.

Codage d’un fichier informatique

Un fichier informatique n’est qu’un tas de bits… des 0 et des 1… comment reconnaitre le contenu ?

Voici des petits logiciel capable de voir le contenu brut d’un fichier:

• HexEd.it… afficher le contenu d’un fichier sous forme hexadécimale. App web
• HxD une application Windows.

Ou tout simplement en ligne de commande:

xxd filename | less

Exercices:

Ouvrir différents fichiers (jpg, png, wave, mp3, txt, php, .exe, html, svg, pdf etc…) et cherchez à décoder leur structures.

Est-ce des fichiers binaires ? texte ? est-ce qu’il y a une entête ? est-ce qu’il y a des métadonnées ?

Que-ce qu’un nombre magique ?

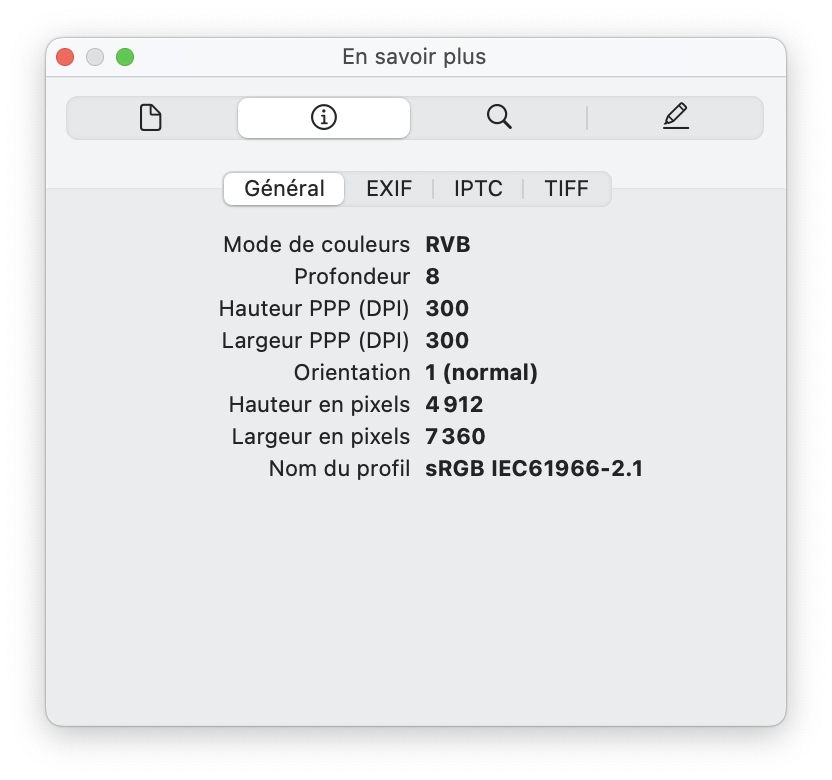
Le format de Métadonnées EXIF est utilisé par les appareils photo pour enregistrer les paramètres de l’appareil au moment de la prise de vue. (Ouverture, temps de pose, date heure, GPS… Ce qui peut jouer des tours…)

Il y a des fichiers dont la base est du texte, et d’autres fichiers qui sont purement du binaire.

Les fichiers .exe soit les fichiers application exécutable de windows sont des fichier purement binaire.

Un fichier html ou CSV, sont des form

ats composés de texte. Ce texte peut être basé sur des encodages parfois différents, comme du ASCII, du latin1 ou de l’UTF-8.

Codage en télécommunication

=> Support de cours pdf: Transmission de données_MButty

Il existe deux grandes famille de code:

• le code de source => décrit l’information => ASCII, UTF-8
• le code de voie => réduit la sensibilité au bruit, ajoute de la redondance et adapte le signal au média utilisé. (niveau électrique et/ou phases pour les 1 et 0) => AMI, Manchester, NRZ

Codage de source

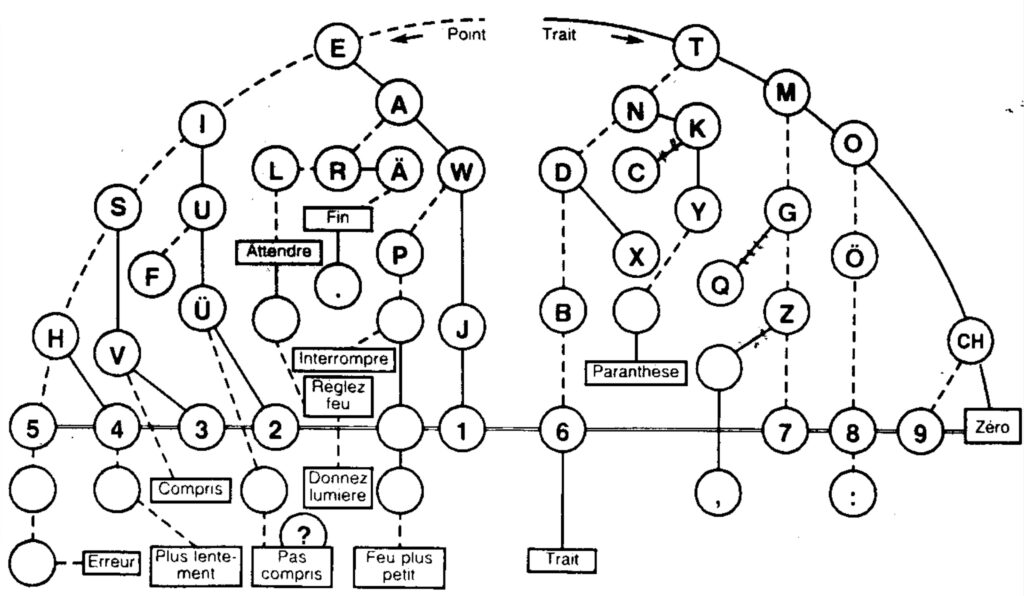
• Code morse => clé codage décodage morse à imprimer
• Code Baudot entre téléscripteurs.
• Code ASCII
• Code EBCDIC utilisé par IBM pour les cartes perforées.
• ISO 8859 Latin 1
• Combinaison de touche ALT
• Code UTF-8
• Base64 et Quoted-Printable.

Historiquement le code ASCII était très utilisé. Mais il ne comporte pas les accents ! Ainsi on a développé plein de code pour chaque langue. On a par exemple le iso 8859-1, le code latin1 utilisé en français. Il est codé sur 8 bits.

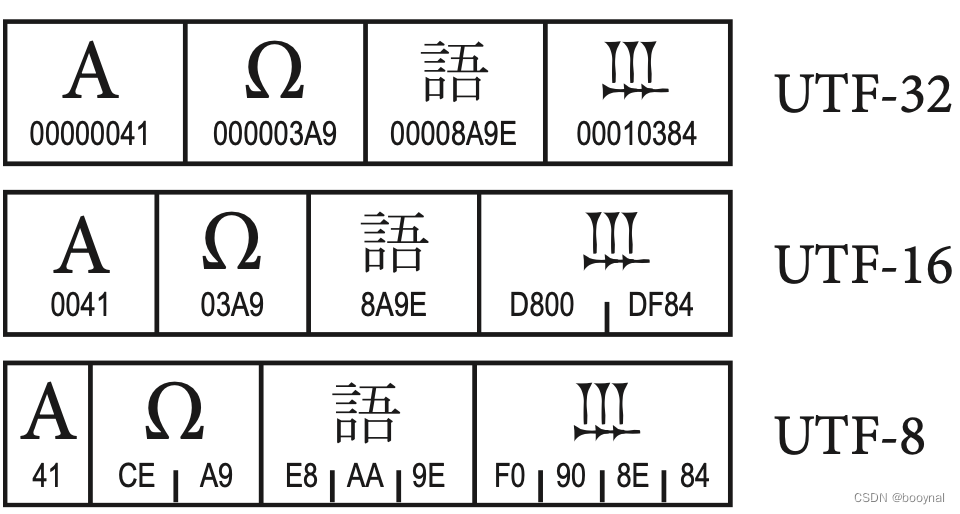
Cependant, avec la mondialisation des échanges. Ce genre de code est limité. C’est ainsi que l’Unicode est arrivé pour coder TOUS les caractères de toutes les langues ! (et les emojii !)

Donc pour coder plus de 150 000 caractères, 8 bits ne suffisent plus ! On passe à 2 octets avec l’UTF-16.

Mais bon, c’est pas pratique l’utf-16, car c’est un nouveau code incompatible. Si une machine ne comprend pas l’utf-16 rien ne s’affiche.

C’est là que l’utf-8 arrive. Il est rétro-compatible avec l’ASCII.
Si l’on veut afficher un caractère qui existait déjà en ASCII on peut toujours le coder sur 7 bits. C’est pareil qu’avant. Et si on nécessite l’affichage d’un caractère qui n’est pas disponible en ASCII, alors le premier octet va indiquer qu’il est suivit d’un autre, et ainsi on construit des « trains d’octet » qui se suivent.

Donc en utf-8, un caractère peut être codé sur un ou plusieurs octets. C’est variable.

Si tu veux tester les possibilités de l’utf-8, tu peux venir apprendre les hiéroglyphes égyptiens avec moi….

Coder de l’information

Ici même j’utilise du texte basé sur un alphabet, mais comment faire le lien entre un dessin et un octet binaire ?

C’est ici que l’on utilise un code. Chaque lettre correspond à un numéro qui est représenté en binaire. Ex: a = 110 0001 (0x61)

Il y a donc évidemment des caractères graphiques « imprimables » qui représentent des lettres, mais aussi des caractères de contrôle, « non imprimable » pour signaler le début et la fin de la transmission, pour émettre un son « Bell » pour la fin de ligne (LF) et retour chariot (CR).

Exercice pratique avec du morse

Exercice pratique de transmission morse avec des fanions (des feuilles de papier suffisent).

Voici un document pdf à imprimer avec une clé de décodage morse et la base des code de contrôle de transmission.

Code ASCII

Le code ASCII est le plus connu pour coder du texte. Chaque caractère tient sur 7 bits. Ce qui permet d’utiliser le dernier bit disponible d’un octet comme bit de parité pour détecter les erreurs de transmission. (voir plus loin pour plus d’info)

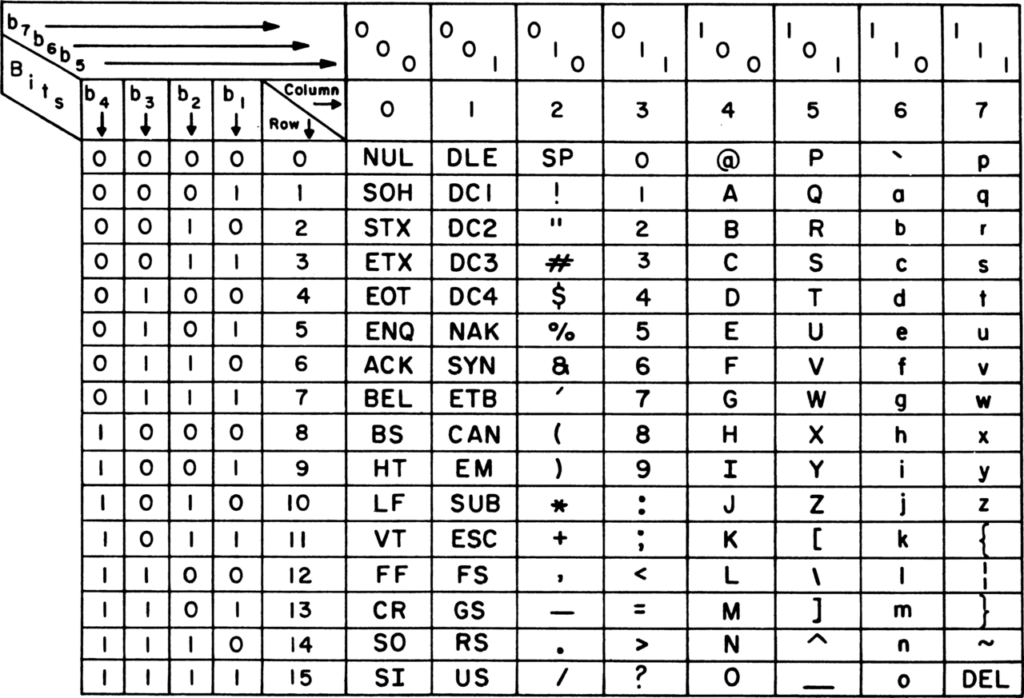
Le code ASCII a l’inconvénient de ne pas supporter les caractères accentués !

De nos jours nous utilisons avantageusement le code UTF-8 pour coder l’information textuelle. Son grand avantage est d’être compatible avec l’ASCII. La base est la même puis, le dernier bit de l’octet sert à indiquer si le caractère est codé sur un octet supplémentaire. On peut ainsi chainer de nombreux octets et créer un très grand nombres de glyphes et symboles. Par ex des hiéroglypes.

Analogie biologique

• ADN n’est pas codée en binaire 0 et 1, mais avec les bases ACGT adénine (A), cytosine (C), guanine (G) ou thymine (T) (et U uracile qui remplace le T pour l’ARN)
• L’équivalent de l’octet 8 bits est le codon, soit une séquence de 3 bases (nucléotides).
• avec 6 bits on a 64 possibilités, avec un codon de 3 bases on a 64 possibilités.
• Chaque codon est traduit en acide aminés protéinogènes. (voir tableau) Ex: GAG = acide glutamique
• Il existe 22 acides aminés protéinogènes sur les 64 possibilités. On a donc des synonymes. On peut écrire de plusieurs manières la génération d’un même acide aminé. Est-ce l’ouverture à la possibilité d’un code de canal (modulation) ?

Voici une explication destiné aux informaticiens qui explique la création du vaccin à ARN message contre le SarsCov.

• ancien lien qui ne répond plus…

• L’ADN, c’est le disque dure
• L’ARN c’est la mémoire vive
• L’ARN messager c’est des « trames », « paquets » qui sont envoyés

• Le code du virus SarsCov-2 et les explications de la structure… (pdf)

Pour en savoir plus, voici aussi la biologie de synthèse qui permet de créer des organismes à partir d’un code source d’ordinateur et d’une imprimante à ADN…

Et bientôt on aura de l’ADN comme support mémoire à long terme. Ça se fait déjà !

Codage de voie

L’information à transmettre est codée en binaire à l’aide d’un code. Le code PCM suffit à être enregistré sur un CD.

Mais dans le monde des télécommunications, on va utiliser des codes de voie (aussi appelé code de canal).

C’est une manière de coder les 1 et les 0 sur un canal de communication. C’est une manière de s’adapter au milieu pour éviter une mauvaise communication.

La transmission simple en « bande de base » des 1 et de 0 comme on le montre dans la vulgarisation ne fonctionne pas très bien. Donc voici des codes de voie utilisés:

• Code Manchester → détecte les flancs montants (0) et descendants (1). Conserve une synchronisation d’horloge.
• Code NRZ → un niveau haut et bas très loin. ex: +12V et -12V
• Code AMI → 3 niveaux de tensions possibles. Le 0 est à 0V le 1 est à une tension haute mais le 1 suivant à la même tension mais inversée (ex: +3V et -3V). On évite ainsi qu’une composante continue du signal ne décale les valeurs et brouille le 0.

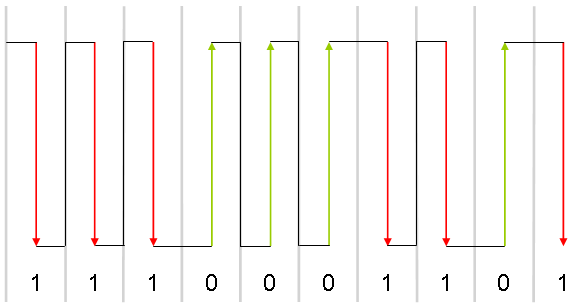
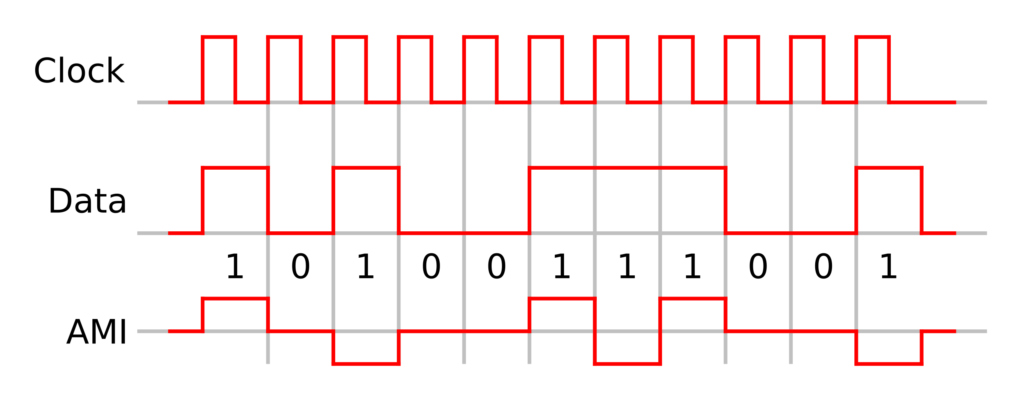
Redondance

Voici des phrases:

• Les oiseaux chantent dans les arbres.
• Non ! Je ne peux pas…

Dans la première phrase, on constate que le pluriel est indiqué avant le mot et à la fin du mot par la marque du nombre. La même information se trouve donc deux fois.

Dans la seconde phrase, la négation est signalée plusieurs fois par des mots différents.

Dans la langue courante, il n’est pas rare de trouver de la redondance d’information. Cette répétition de la même information permet de confirmer le sens de la phrase. Si un mot est perdu à cause d’une perturbation, le sens général de la phrase reste.

Compression de données

La fréquence d’apparition des lettres dans une phrase ne sont de loin pas identiques. En français on trouvera beaucoup plus souvent la lettre « e » que la lettre « k ».

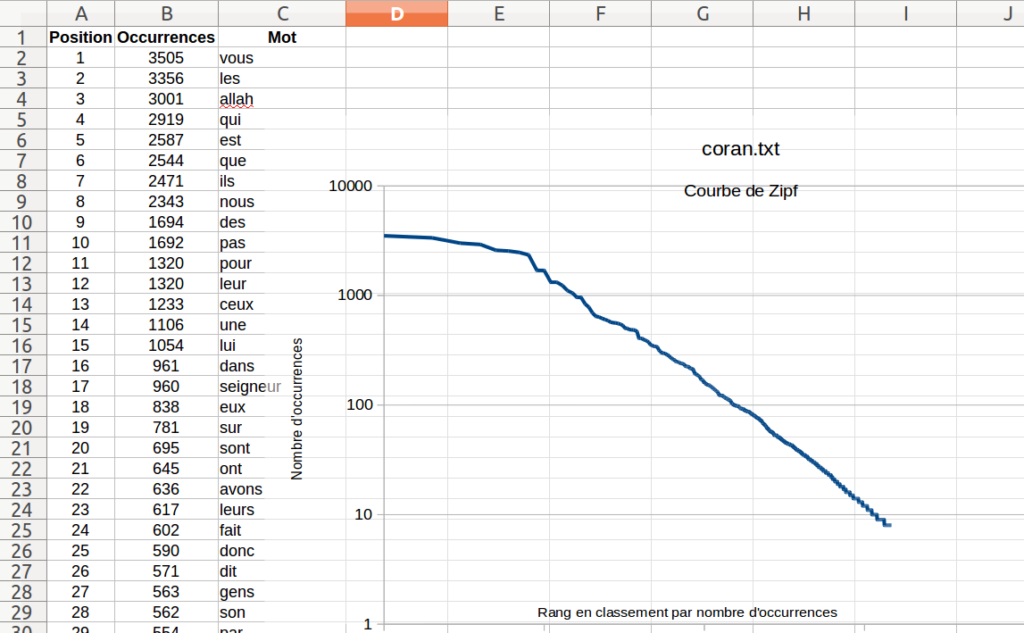
George Kingsley Zipf a entrepris le livre James Joyce, Ulysse, et d’en compter les mots distincts, puis de les présenter par ordre décroissant du nombre d’occurrences.

La légende dit que Zipf a obtenu un résultat du type:

• le mot le plus courant revenait 8 000 fois
• le dixième mot 800 fois
• le centième, 80 fois
• et le millième, 8 fois

C’est devenu la Loi de Zipf.

Compression non destructive de données

En s’inspirant de la loi de Zipf, l’idée principale de la compression (non destructive) de données, c’est d’attribuer un code court aux lettres fréquentes.

Le morse applique clairement cette idée en utilisant le point: « . » comme code pour le « e ».

C’est ainsi qu’est né le format ZIP de compression sans perte (et archivage) de fichiers.

Le format ZIP se base sur l’algorithme du codage de Huffman.

Cet algorithme est un code à longueur variable. Au lieu d’avoir toujours le même nombre de bit par caractère. (ex: 8 bits par caractère) Le codage de Huffman va établir un « dictionnaire » de codes de longueur variable. La taille du code binaire dépend de la fréquence d’apparition du caractère dans le contenu.

Par exemple un « e » – lettre la plus fréquente en français – va être codée avec un code court. Par exemple: « 1 » et la lettre K plus rare sera par exemple codée avec un code plus long, par ex: 1001

Pour déterminer le code binaire et sa longueur on va utiliser une structure de donnée en arbre, et suivre un petit algorithme de construction:

• Chaque lettre d’une suite de caractère est associée à son nombre d’occurrence. ex: a:10 fois, c:4, f:8
• Ceci nous donnes les feuilles d’un arbre (vert)
• L’arbre est construit des feuilles à la racine par association de « feuille » (ou branche) de valeurs « similaires ».
  • On choisi les deux valeurs les plus petites. (ex: b:7 et d:5 ou encore c:4 et e:4)
  • On relie les deux feuilles par un embranchement libellé avec la sommes de deux feuilles. (ex: b:7 + d:5 = :12) et (c:4 + e:4 = 8)
  • On recommence l’opération jusqu’à obtenir une racine unique.
• On associe ensuite un code binaire à chaque embranchement de l’arbre.
• Comme c’est du binaire, il suffit d’associer 0 à un embranchement et 1 à l’autre.
• La lecture du code associé à chaque caractère se lit en suivant les embranchement de l’arbre de la racine à la feuille dont on cherche le code.
• ex: racines- 0-1-0 nous mène à la feuille b : 7. Donc b → 010

Pour l’arbre présenté dans la vidéo ci-dessus on obtient un « dictionnaire » de code suivant:

• a : 00
• b : 010
• c : 100
• d : 011
• e : 101
• f : 11

Le décodage se fait tout simplement en suivant la suite des nombre binaires sur l’arbre associé. A chaque fois qu’on arrive sur une feuille, on note la lettre trouvée et on recommence depuis la racine.

C’est quasi « magique », car malgré la longueur variable du code on retrouve chaque lettre sans savoir où sont les séparations. (il faut quand même connaitre l’arbre !!)

C’est typiquement le genre d’algorithmes de compressions sans perte utilisés pour les formats Zip, RAR, gzip, 7-Zip, xz…

On reconnait le même principe que pour la clé de décodage morse, l’arbre est construit selon la fréquence des lettres. Plus une lettre est courantes, plus elle est représentées par un code court.

En savoir plus sur la compression de données sans perte.

Compression destructive

Les données brut d’un enregistrement continent parfois plus d’information que nécessaire pour une bonne expérience de visualisation.

Ce genre d’algorithme est basé sur les perceptions humaines. Par exemple, l’oeil humain est peu sensible aux forts contrastes dans une image.

Ainsi il est possible d’atténuer ces contrastes pour diminuer la taille des données.

Algorithme JPEG

C’est ce que pratique par exemple l’algorithme du jpeg. En pratique, un fort contraste, c’est une haute fréquence dans la représentation spectrale des données. Donc cet algorithme va transformer les données en représentation spectrale, supprimer les hautes fréquences et revenir en représentation spatiale.

Voici une bonne description de cet algorithme du JPG…

Les étapes de l’algorithme jpeg:

• Conversion de l’image dans la représentation Y’CbCr (luminance + Chrominance (y -bleu et y -rouge) )
• Sous-échantillonnage de la chrominance
• Transformée en cosinus discrète (une sorte de transformée de Fourrier discrète)
• Quantification
• Parcours en zigzag du quadrillage de données
• Algorithme de Huffman pour compresser sans perte le tout

Algorithme PNG

L’algorithme de compression jpeg fonctionne bien pour les photos. Il « adoucis » les photos en lissant les contrastes.

Par contre si l’image contient de forts contrastes, comme pour une image d’un texte, ou pour un logo. L’algorithme jpeg va créer des bavures.

Ainsi on va utiliser un autre algorithme. Une des caractéristiques d’un texte ou d’un logo c’est de comporter très peu de couleur. Donc pourquoi utiliser 32 bits d’information par pixel quand seulement 1 bits suffit à coder noir ou blanc ?

L’algorithme du format PNG va donc réduire l’espace des couleurs à disposition pour compresser l’image.

Principe de codage des couleurs d’un pixel

Pour bien comprendre, revenons sur le principe de codage d’une image.

Une image c’est une grille de pixels, on parle d’image « matricielle ». Chaque pixel représente une couleur. Cette couleur doit être codée en bit d’information.

Généralement on code les couleurs en représentation RVB, soit un mélange de proportion de Rouge, Vert et Bleu.

Chaque pixel est codé sur 32 bits. (4 octets) Mais très souvent seuls 24 des 32 bits sont utilisés, comme c’est le cas pour le format bitmap .BMP

Les 24 bits (3 octets) sont décomposée en 3 fois 8 bits:

• 8 bits de rouge
• 8 bits de vert
• 8 bits de bleu

Soit 2⁸ = 256 niveaux par couleur primaire.
Ce qui nous donne 2²⁴ ou 16 777 216 couleurs différentes possible pour chaque pixel.

La représentation des couleurs se fait souvent en hexadécimal (c’est trop long et source d’erreur d’utiliser la notation binaire). Donc chaque couleur primaire est exprimée par 2 caractères.

FF FF FF → 100% Rouge + 100% Vert + 100% Bleu = Blanc
00 00 00 → 0% Rouge + 0% vert + 0% Bleu = Noir
FF FF 00 → 100% Rouge + 100% Vert + 0% Bleu = jaune
66 DD AA → 20.69% Rouge + 44.83% Vert + 34.48% Bleu = Medium Aquamarine

Dans les caractéristiques des images, on parle de profondeur pour indiquer le nombre de bits sur lesquels une couleur est codées.

En PNG, il existe donc plusieurs profils de représentation des couleurs:

• 1 bit donc deux couleurs
• 2 bits en 4 couleurs basiques
• 4 bits permettant de choisir parmi une palette de maximum 16 couleurs contenues dans le fichier
• 8 bits en niveaux de gris (256 niveaux)
• 8 bits permettant de choisir parmi une palette de maximum 256 couleurs contenues dans le fichier (équivalent au format GIF)
• 24 bits, soit 2²⁴ ou 16 777 216 couleurs (couleurs vraies, 256 couleurs par canal RVB).
• 32 bits, soit 2³² ou 4 294 967 296 couleurs.
• 48 bits, soit 2⁴⁸ ou 281 474 976 710 656 couleurs.

Les trois derniers ne sont plus tellement de la compression de données, mais juste une codage d’image.

Si seuls 3 octets sur les 4 octets sont utilisés, pour coder une image, il est assez aisé de réduire la taille d’un fichier BMP. En revanche, le format PNG utiliser le dernier octet pour coder une notion de transparence.

Mais.. on peut aussi faire d’autres choses avec un octet inutilisé par pixel…

Stéganographie

• Détection de stéganographie…
• Outil online d’encodage-décodage de stéganographie…
• OutGuess…
• exemple de chasse aux trésor utilisant de la stéganographie… Cicada 3301… voici une bonne vidéo de vulgarisation à propos de Cicada 3301…

Image vectorielle

Une image vectorielle n’est pas composée d’une grille de pixels, mais c’est une image numérique composée d’objets géométriques individuels, des primitives géométriques (segments de droite, arcs de cercle, courbes de Bézier, polygones, etc.)

Le format vectoriel du web s’appelle le SVG.

<?xml version="1.0" encoding="utf-8"?>
<svg xmlns="http://www.w3.org/2000/svg" version="1.1" width="300" height="200">
  <title>Exemple simple de figure SVG</title>
  <desc>
    Cette figure est constituée d'un rectangle,
    d'un segment de droite et d'un cercle.
  </desc>
 
  <rect width="100" height="80" x="0" y="70" fill="green" />
  <line x1="5" y1="5" x2="250" y2="95" stroke="red" />
  <circle cx="90" cy="80" r="50" fill="blue" />
  <text x="180" y="60">Un texte</text>
</svg>

Voici ce que donne le code ci-dessus:

L’avantage des images vectorielles c’est de pouvoir redimensionner les images facilement sans perte de qualité vu qu’on est pas lié aux pixels.

Compression de données Audio

Dans le domaine de l’audio, les principes sont similaires à ceux du domaines de l’image.

On a des fichiers WAV, AIFF, qui sont non compressé. (du PCM brut voir plus bas pour le détail de la conversion de son analogique en numérique).

Nous avons aussi le format Flac qui est compressé mais de façon non destructive. Le FLAC obtient des taux de compression des données PCM de 30 à 70 %. C’est mieux que de juste appliquer une compression ZIP qui atteint 20 à 40 %.

En effet, le ZIP est un algorithme de compression sans perte généraliste. Il ne tient pas compte de la nature des données compressée. Le FLAC utilise une prédiction linéaire sur des blocs de 100ms, codage par plages qui est efficace pour coder les silences et les blancs. (par ex, en indiquant 1 seule fois le blanc vu qu’ils sont tous identiques et en y faisant juste référence quand on en trouve un.)

Puis nous avons la famille des algorithmes de compression destructive. Le format le plus connus est le MP3.

Les autres formats courants sont le AAC et le Vorbis.

On est dans la même idée qu’avec le jpeg, il s’agit de se baser sur les perceptions acoustiques des humains. Les fréquences qui nous sont moins audibles sont supprimées.

Exercice de récapitulation:

Avec quel algorithme de compression de données faut-il compression un logo en 4 couleurs ?

Avec quel algorithme de compression faut-il compresser une photo ?

A quelle couleur correspond le code binaire: 111110111101000010010111 ?

Compression des fichiers déjà compressés

Est-ce que créer une archive ZIP d’un dossier de photo jpeg va diminuer la taille mémoire de l’archive ?

Une fois qu’une image est déjà compressée, on ne peut théoriquement plus la compresser encore une fois. On va même avoir l’effet inverse, avec toutes les entêtes et dictionnaire créé pour compresser le fichier.

Si c’est une compression destructive, on va même détruire petit à petit un peu plus les données, un peu comme on le faisait en analogique.

C’est l’effet photocopieuse.

Voici un exemple d’une vidéo envoyée sur youtube (donc compressée) puis téléchargée, et remise sur youtube donc compressée à nouveau, et on recommence la boucle un bon millier de fois….

Cette expérience nous montre que youtube recompresse les vidéos à chaque fois.

Correction d’erreur

Le principe fondamental de la correction d’erreur c’est d’ajouter de la redondance. De l’information supplémentaire qui permet de retrouver ce qui manque. Au pire, indique qu’il y a une erreur, ce qui permet de demander une retransmission de l’information.

Au mieux, l’idée est de pouvoir reconstruire l’information qui s’est perdue dans le canal de communication.

En français on utilise le même principe. Voici un exemple de phrase avec de l’information redondante:

• Non ! Je ne peux pas…

La négation est clairement exprimée de 3 façon différentes !

Bit de parité

L’ajout d’un bit de parité est le principe le plus simple pour détecter une erreur, mais ne permet pas de corriger l’erreur.

Le bloc de données concerné doit toujours avoir un nombre de bit à l’état 1 qui est pair. (ou impair, en fait c’est un choix)

Généralement on transmet des données octet par octet. Ainsi on peut utiliser:

• 7 bits de données (code ASCII par exemple)
• 1 bit de parité qui est choisi pour garantir un nombre pair de 1

Si l’octet reçu a un nombre pair de bit à 1. → transmission OK
Sinon, une erreur est arrivée. On bloque tout ou on demande la retransmission.

exemple:

01110010 → 4*1 → pair → ok
11010101 → 5*1 → impair → erreur !

La vérification d’un octet consiste à faire une somme des bits, ainsi ce genre d’algorithme de détection d’erreur est communément appelé une somme de contrôle.

On utilise toujours cette terminologie pour des autres algorithmes plus complexe qu’une somme. Par exemple:

• Les empreintes (Hash) MD5 ou SHA-1, sorte de résumé d’un gros fichier en une chaine de caractère.
• CRC → Contrôle de Redondance Cyclique. Le FCS utilisé dans les trames Ethernet.

Code de répétition

Pour corriger une erreur, un des code le plus simple et le code de répétition. On va augmenter la redondance. On va coder chaque bit plusieurs fois.

Par exemple on code chaque bits 3 fois et le décodage se fait en choisissant l’état majoritaire:

111 000 111 001 010 111 000 000 110 111 010 111

En gras, les bits d’erreur que l’on corrige..

C’est une méthode efficace. Mais ça demande beaucoup de ressources de tripler la quantité d’information à transmettre. Est-ce qu’il existe une technique moins gourmande et tout autant efficace ?

C’est là que la théorie de l’information et la théorie des codes se sont construites pour répondre de façon formelles à ce genre de questions.

Convention en théorie de codes

En théorie des codes, on utilise les conventions suivantes:

• C est le code composé de M mots (de dimension M)
• M est le nombre de Mots de code qui composent le code C.
• n est la longueur d’un mot M

On peut ainsi caractériser un code en le nommant: (n, M)

Pour le décodage on ajoute:

• d qui est la distance minimale entre deux séquences de symboles.

On peut ainsi préciser notre caractéristique de code: (n, M, d)

Code correcteur de Hamming

Le code de Hamming est un code correcteur d’erreur. Comme la parité, il permet de détecter une erreur. Mais en plus, il permet de corriger une erreur.

Un vendredi de 1947 Richard Hamming a lancé une série de calculs à effectuer pendant le week-end sur des calculateurs numériques. Le lundi, il revient et des erreurs de communication ont interrompu le calcul.

A l’époque on utilise un bit de parité, mais pas de correction d’erreur. Hamming décide de trouver un moyen de corriger les erreurs et ainsi de pouvoir laisser tourner des ordinateurs pendant les week-ends sans soucis.

Il crée donc toute la famille des codes de Hamming, dont le code de Hamming (7,4). (n, M)

Donc pour un message de 7 bits de long, ce code transmet 4 bits utiles de données et il utilise 3 bits de parité pour ajouter la redondance nécessaire à corriger 1 bits d’erreur.

Au lieu d’utiliser un bit de parité pour chaque bloc, on va mutualiser les bits de parités pour les utiliser pour plusieurs bits en même temps. Ainsi on obtient le minimum de bits de parités possible.

Distance de Hamming

Une notion importante est la distance de Hamming entre deux codes. C’est le nombre de modifications qu’il faut pour passer d’un code à un autre. (donc potentiellement le nombre d’erreurs produites pour qu’un code se transforme et ressemble à un autre)

Dans un code binaire de base, si j’ai une seule modification d’un 0 en 1, je change le code, je tombe sur une autre valeur possible, et il m’est donc impossible de savoir si une erreur à eu lieu, car toutes les possibilités sont plausibles.

Le code binaire comme le code ASCII ont donc une distance de Hamming de 1.

Il est possible de détecter « la distance de Hamming » – 1 erreur.

Si je veux pouvoir détecter une erreur, je dois ajouter de l’information. Si j’ai une modification d’un bit et que je tombe dans une sorte d’état interdit, je saurais qu’il y a une erreur.

Si j’ajoute un bit de parité j’ai une distance de Hamming = 2
=> Je peux donc détecter 2-1 = 1 erreur.

nombre	binaire	Parité impaire
0	000	0001
1	001	0000
2	010	0100
3	011	0111
4	100	1000
5	101	1011
6	110	1101
7	111	1110
Distance de Hamming:	1	2

Si je veux pouvoir corriger une erreur, il me faut encore ajouter de l’information. Si j’ai une modification d’un bit et que je détecte un état interdit et le chemin qui y a permis que j’y arrive, je peux corriger l’information.

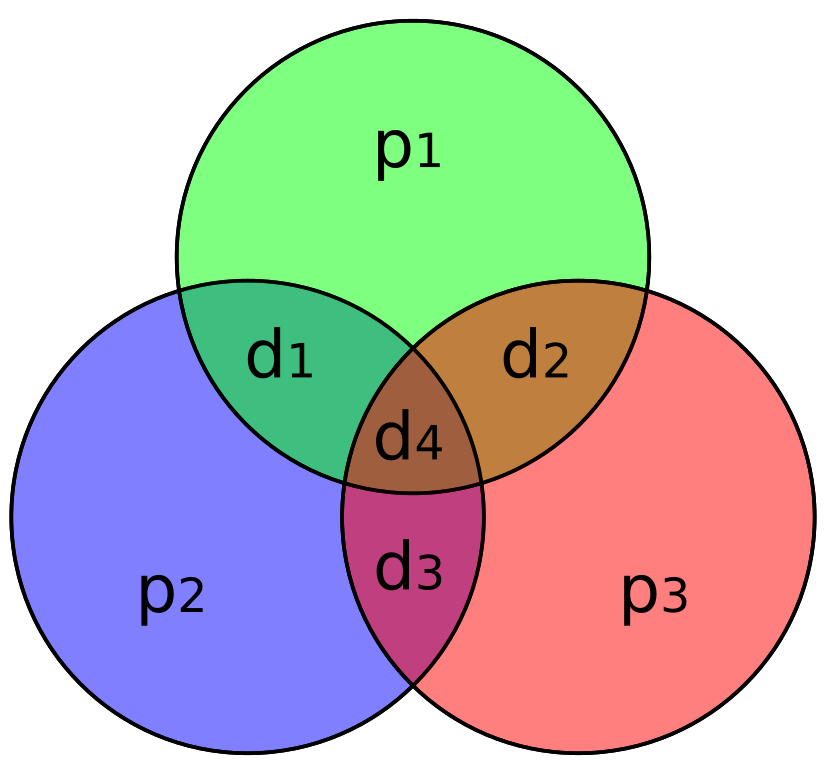
Dans le dessin ci-dessous, on code des lettres avec des codes binaires de 4 bits. (de 0000 à 1111 donc 16 possibilités, on peut faire de l’hexadécimal)

Ce dessin permet de représenter les chemins possibles pour la modification d’un code à un autre.

• Le chemin rouge a une distance de hamming de 2 (1100 nécessite 2 bits changés pour arriver à 1000)
• Le chemin bleu a une distance de hamming de 1 (0110 nécessite le changement d’un bit pour arriver à 1110).

Il est possible de corriger (« la distance de Hamming » – 1)/ 2 erreurs.

Voici comment encoder un message binaire avec le code de Hamming et comment le décoder et corriger les erreurs éventuelles.

Nous allons donc créer un certain nombre de bits de parité.
Le nombre de bit de redondance r doit vérifier l’équation 2^r >= le nombre de bits de data + r + 1.

Donc pour un message de < = de 4 bits → r = 3 → le code est le hamming 7-4
Puis les codes, 15-11 ou 3126 ou 127-120 ou 255-247

La grande astuce consiste à placer les bits de parités logiquement.
C’est finalement une logique assez comparable à celle que l’on utilise pour construire une table de vérité binaire. On va placer les bits de parité sur les positions de mon message qui sont des puissances de deux.

Pour le détail voici une explication en vidéo:

La fonction OU exclusif, indiquée XOR est un détecteur d’état différents. Donc on peut l’utiliser pour vérifier le bit de parité.

= « L’un ou l’autre, mais pas les deux ».

Cette fonction logique est presque comme le OU, mais quand les entrées sont à 1 il faut choisir… comme pour le mariage, c’est l’une ou l’autre mais pas les deux ! On ne peut pas avoir deux femmes en même temps !

Entrée		Sortie
A	B	A XOR B
0	0	0
0	1	1
1	0	1
1	1	0

Conversion analogique numérique

Le monde à notre échelle est analogique. Pour avoir un signal numérique il est donc nécessaire de le convertir en numérique.

Voici en vidéo les explications de la différence entre l’analogique et le numérique.

Pour convertir un signal analogique en signal numérique, il y a deux étapes importantes:

• l’échantillonnage
• la quantification

Le nombre de niveaux disponibles – donc la précision du son – dépend du nombre de bit sur lesquels ont quantifie le signal.

Voici un aperçu du son quantifié sur 8 Bits:

Le son 8 Bits est une sort de son « pixelisé ». C’était la capacité maximale des console de jeu d’il y a 40 ans…

Actuellement on quantifie la musique sur 16 bits pour un son excellent (qualité CD). Mais malgré tout il y a des fans de son 8 bits. C’est devenu un style.

Echantillonnage

Pour le convertir en numérique on va échantillonner le signal analogique. C’est à dire qu’on va régulièrement prendre une valeur du signal.

Plus on prend une valeur souvent, plus on va être précisé. Mais grâce au théorème de shannon et nyquist on peut limiter la fréquence d’échantillonnage.

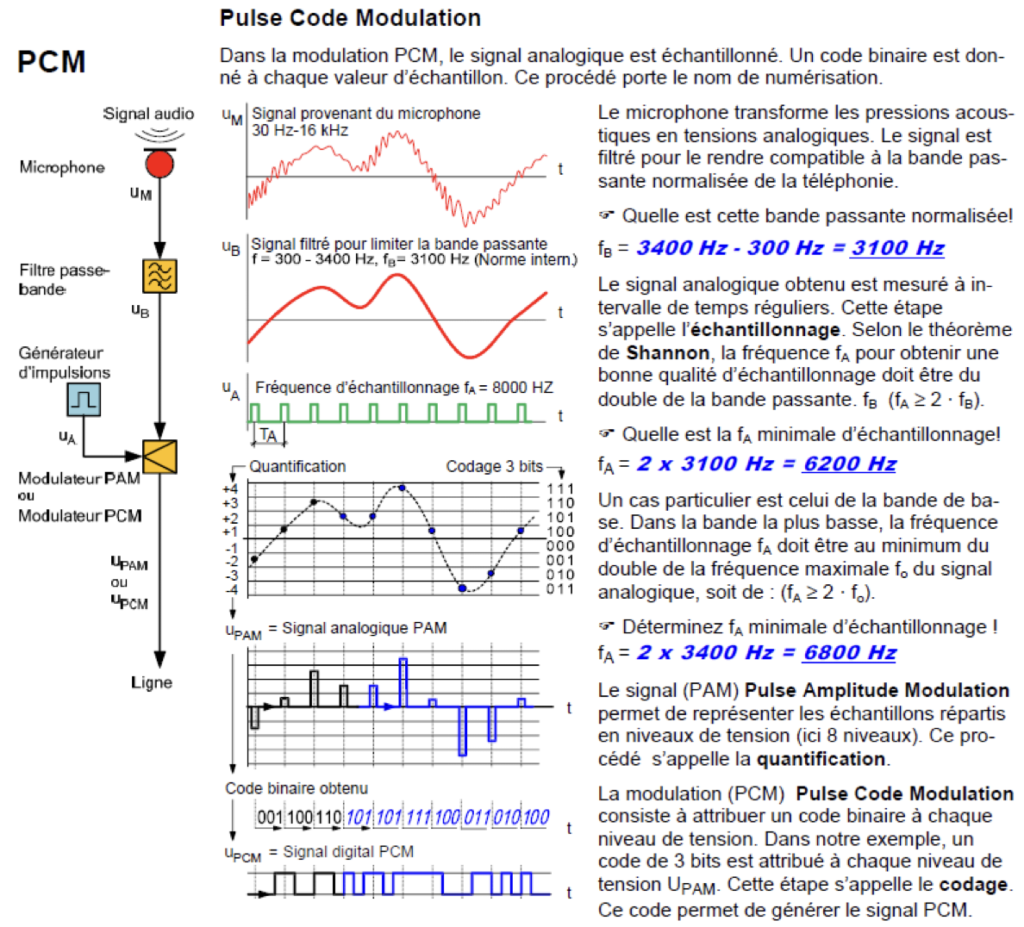
Le théorème de l’échantillonnage nous dit que la fréquence d’échantillonnage doit être d’au moins 2 fois la fréquence maximale du signal.

La bande passante, c’est la largeur de fréquence (de la plus petite à la plus grande) qu’on observe dans le spectre d’un signal.

Dans une téléphone, on fait passer des fréquences de 300 à 3400Hz. Ainsi on a une bande passante de 3100Hz, et une fréquence maximale de 3400Hz.

Donc la fréquence minimale d’échantillonnage pour pouvoir reconstituer une signal sera de 2*3400 = 6800 Hz.

Pour le téléphone, la norme minimale a été placée à 8kHz.

Petit calcul, donc tous les combien de temps on va prélever un échantillon si l’on utilise une fréquence de 8kHz ?

T = 1/f

A propos de Spectre d’un signal… voici le logo de l’entreprise Cisco très active dans les réseau de télécommunication.

Hormis le fait que cette entreprise est basée à San-FranCISCO… est-ce que ça vous rappelle quelques chose ?

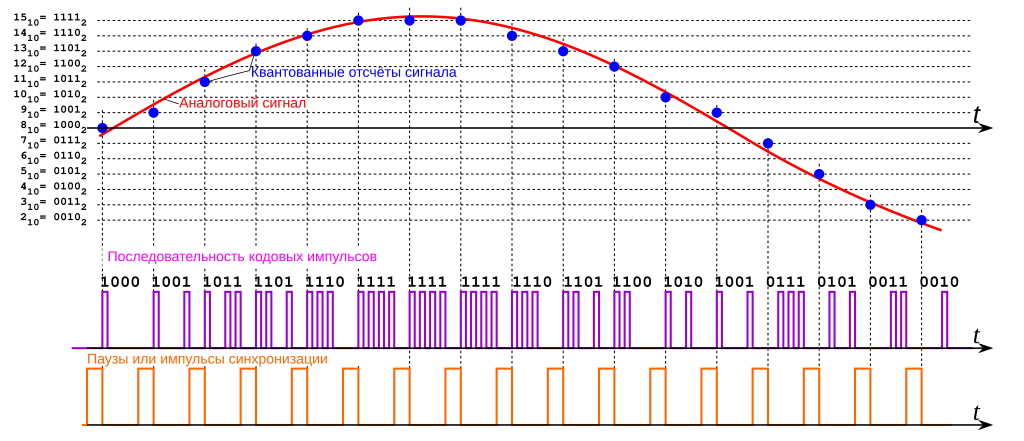
Quantification

Avec l’échantillonnage on va prélever une information un certain nombre de fois par seconde.

Puis il faut enregistrer sa hauteur, sa valeur. On va donc quantifier la hauteur d’un signal avec un niveau.

Pour ce faire, il nous faut définir une échelle de hauteur. Comme nous travaillons en binaire, la précision de cette échelle va dépendre du nombre de bits utilisés.

Sur le schéma ci-dessus, nous utilisons 3bits pour expliquer le principe.

Combien de niveaux différents peut-on avoir avec une valeur définie sur 8bits ?

Si l’on a une fréquence d’échantillonnage de 8kHz et un niveau de quantification exprimé sur 8 bits, quel est le débit binaire dont nous avons besoin pour transmettre ce signal en numérique ?

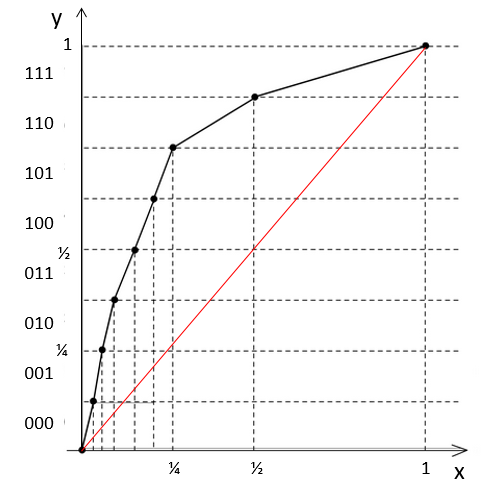
Quantification non linéaire

ci-dessus on a vu comment on peut quantifier la hauteur d’un signal avec des niveau réparti sur une échelle linéaire régulière.

Or, il existe d’autre manière de faire. On peut réduire le nombre de niveaux en codant la hauteur avec une échelle qui n’a pas des intervalles réguliers.

C’est ce que l’on pratique pour l’audio, particulièrement pour la téléphonie.

Comme notre perception des sons est logarithmique il fait sens d’utiliser une échelle logarithmique. Par exemple, si j’ai un micro avec une tension qui sort du micro et représente un son. Je suis capable de faire la différence entre une tension de 0,3V et une tension de 0,4V. Par contre je suis incapable de faire la différence entre une tension de 4,3V et une tension de 4,4V, pourtant en absolu c’est le même écart. Plus le niveau augmente, moins je perçois les différences.

Donc pour économiser de l’information à transmettre, on va utiliser une échelle logarithmique pour créer les niveaux. Ainsi on va « compresser » les hauts niveaux un peu plus. La voix est toujours compréhensible pour le téléphone, mais ainsi au lieu de d’avoir besoin de 14 bits pour notre codage, 8 bits suffisent.

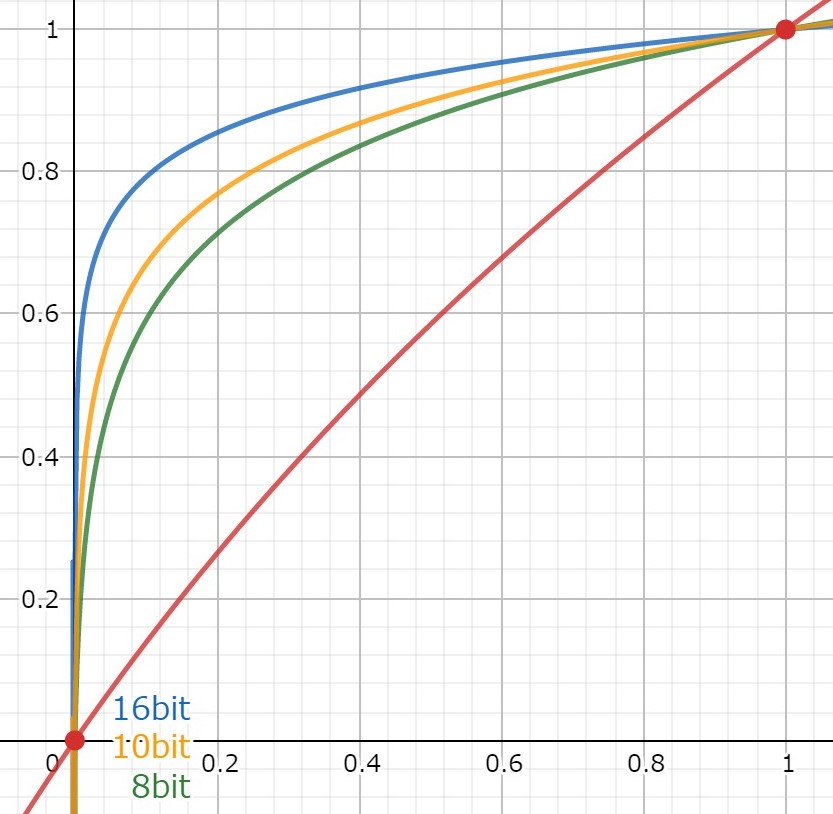
On le voit bien sur le schéma ci-dessus. Une faible variation sur l’axe horizontal donnera des codes différents si l’on est proche du niveau 0 à gauche. En revanche sur la moitié droite de l’axe horizontal, une variation de la même ampleur que précédemment donne le même code.

Comme souvent, il y a des pratiques différentes entre les USA et le reste du monde.

Ainsi la compression logarithmique se fait:

• Avec la loi µ aux USA et au Japon
• Avec la loi A Europe et dans le reste du monde.

Modulation PCM

Une fois que l’on a échantillonné et quantifié le signal, il faut coder l’information. La méthode la plus simple est ce qu’on appelle la PCM, Pulse Code Modulation.

Cette méthode nom compressée, est le format de donnée que l’on retrouve majoritairement dans les fichiers audio de type WAV, AIFF ou BWF.
Attention tout de même, ce genre de fichier sont des conteneurs, ils peuvent contenir aussi d’autres formats, donc il faut lire l’entête du fichier pour savoir quel code est véritablement utilisé.

Le codage PCM est aussi celui qui est utilisé sur les CD audio, avec une fréquence de 44,1kHz et une quantification sur 16 bits.

Ecouter le silence

Expérience de trouver le silence dans le flux RTP d’une conversation VOIP…

Téléchargez un fichier de capture wireshark… conversation G711.pcap

Le silence est représenté sous la forme de l’hexadécimal: D5

Codec

Codage – Decodage

Voici les caractéristiques principales des codes que l’on utilise en téléphonie.

G.711
→ échantillonnage sur 8kHz
→ bande passante 300 – 3400 Hz
→ loi A ou loi mu pour la quantification logarithmique. (13 ou 14 bits ramené à 8)
→ 64 ou 56 kbit/s
→ code PCM (Modulation Impulsion Codées)
→ code Manchester possible pour PCM → on conserve l’horloge. Le flan haut à bas = 1 et bas à haut = 0 (ou l’inverse)
(en ISDN on utilise un code ternaire, à 3 tensions, il y a violation de l’alternance pour indique le début de la trame)

G.722
→ qualité haute définition par rapport à G.711 → On a augmenté la bande passante
→ bande passante 50 – 7000 Hz
→ 16kHz d’échantillonnage
→ ADaptivePCM → MICDA
→ 64 kbits/s

G.722.2
→ 16kHz d’échantillonnage
→ bande passante 50 – 7000 Hz
→ débit réseaux 6,6 à 23,85 bit/s

G.726
→ ADPCM à 40, 32, 24 ou 16 kbit/s.

G.729
→ codage de parole à 8kbit/s par prédiction linéaire avec excitation par séquences codées à structure algébrique conjuguée.
→ débit réseau: 32.8 kbits/s

Pour étudier les réseaux de téléphones de Nouvelle Génération, ainsi qu’écouter les différences de qualité des codec. (Menu: Protocoles > RealTime Transport Protocole….)

Pourquoi est-ce que l’on privilégie le numérique à l’analogique ?

Voilà après avoir observé la quantité massive de données que produit le numérique, pour un signal tronqué, qui n’est pas complet, une question subsiste: pourquoi est-ce que l’on fait tout ça ?

Pourquoi est-ce que l’on s’embête à passer au numérique ?

Modulation

La modulation d’un signal permet de transporter un signal sur une plus longue distance qu’il ne pourrait le faire directement. (en bande de base)

Par exemple, un signal d’un réseau informatique LAN Ethernet ne peut aller au delà de 100m. Ainsi pour se connecter à Internet via une ligne de téléphone, on passe par une modulation. On utilise le protocole VDSL.

Grâce à la modulation on peut ainsi passer d’une portée de 100m à plusieurs kilomètres. (~3Km avec du VDSL2)

On va moduler une porteuse capable de faire le chemin avec notre petit signal.

C’est exactement ce que fait un Modem (modulation-demodulation) VDSL.

Pour la transmission par onde radio on utilise aussi beaucoup les modulations. Si on envoyait directement le signal d’un micro par les ondes hertziennes on ne pourrait faire de la radio très loin. Donc on utilise une modulation.

La modulation est un mélange de 2 signaux:

• le signal d’information utile
• la porteuse

Lorsque l’on veut écouter une station radio, on sélectionne sa fréquence porteuse sur le poste de radio. Par ex: 90.4 MHz pour fréquence Banane. (1 mois par an)

Voici une liste de fréquences radio utilisée dans la région neuchâteloise.

Les types de modulations

Il existe plusieurs manières de mélanger un signal et une porteuse. Historiquement c’est la modulation d’amplitude AM qui s’est faite en premier, puis a suivi la modulation de fréquence FM.

Depuis 2025, la RTS ne diffuse plus en FM, il faut écouter la radio en DAB+.

Au fil du temps, on est passé de la modulation analogique à la modulation numérique.

• FSK – Modulation par déplacement de fréquence
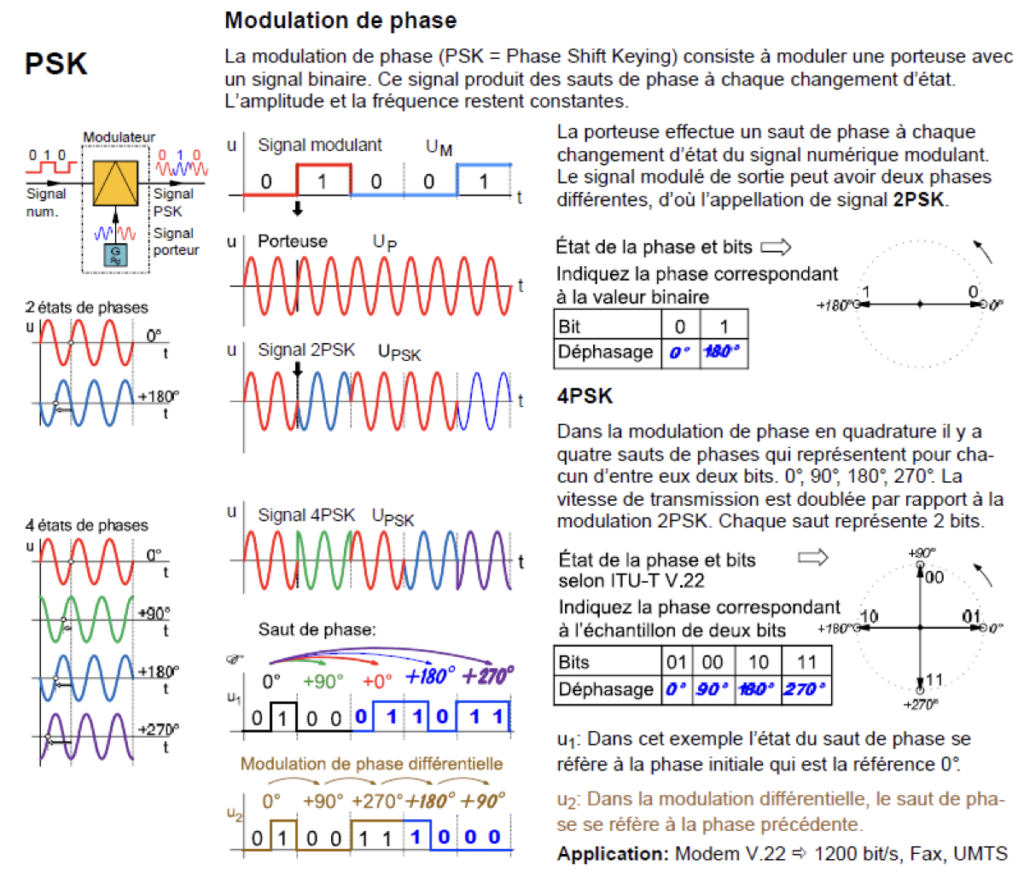
• PSK – Modulation par changement de phase
• QAM – Modulation d’amplitude en quadrature

Diagramme de constellation utilisé surtout en CATV pour mesurer la qualité de la transmission.

Chiffrement