Math pour IBAT – Informaticiens du bâtiment

Supports de cours

Voici les supports de cours fourni par eit sur la plateforme.

Cours de Math Télématicien CPBM
Cours de math pour électriciens → Corrigé

Supports de cours avec corrigés

Table des matières

60 – Statistiques
70 – Physique mécanique
100 – Optique

60 – Statistiques

« Les statistiques c’est comme les bikinis… ça montre beaucoup de choses, mais ça cache l’essentiel… »

Objectifs

Compréhension des notions de base du calcul des probabilités et des statistiques
Aptitude à calculer les probabilités d’occurrence
Connaissance des distributions de probabilités les plus importantes et leurs grandeurs caractéristiques
Capacité d’évaluer de manière critique des données statistiques
Capacité de simuler des expériences de probabilités

A quoi ça sert les statistiques ?

Voici une série d’exemple de diverses formes de statistiques:

Worldometer, des compteurs sur la population mondiale et autres…
Statistiques COVID du canton de Neuchâtel
Statistiques sur les votations du 19.11.2020 à propos des multinationales responsables.
Statistiques à propos des communes suisses par Martouf. (surface, population, densité, forêt, étrangers, partis politique, etc..)

Densité de population par commune en 2019

Vidéos d’explication des statistiques

Voici une playlist d’une série de vidéos qui explique les base de la statistique.

Exercice des quartiers de mandarine

Pour voir apparaitre une distribution statistiques, faisons une expérience. Combien y a-t-il de quartiers dans une mandarine ? (et dans une orange ?)

On devrait voir apparaitre une loi normale…

Voici ce que j’observe….

J’ajoute une coche à chaque fois que je compte le nombre de quartiers:

06 → |
07 →
08 → |||||||||||||||||
09 → |||||||||||||||||||||||||||
10 → |||||||||||||||||||||||||||||||||||||||||||||||||||||||
11 → |||||||||||||||||||||||||||||||||
12 → ||||||||||||||
13 → |||||
14 →||
15 →
16 → | (variété de zanzibar !)

Ah.. voici encore une autre stat….

Exercice du lancé de dé…

Voici un dé virtuel…

Faites un histogramme à chaque lancé de dé. Qu’est-ce qu’on observe ?

Définitions et symboles

${\bar {x}}$ (x barre ou x avec un macron) → moyenne arithmétique (la moyenne la plus courante, celle qu’on utilise pour la moyenne des notes !) C’est aussi la moyenne d’un échantillon d’une population. (on connait toutes les valeurs d’un échantillon, mais pas de la population qu’il représente)
μ (mu) → La moyenne de la population d’une distribution. C’est la moyenne extrapolée d’une population sur la base de quelques moyennes d’échantillon les plus représentatifs possibles. (on va pas mesurer la totalité des 8 milliards d’humains pour connaitre la taille moyenne d’un humain, un échantillon suffira.) Pour le cas particulier de la loi normale, μ c’est aussi l’espérance, le mode et la médiane !!! (oui tout est confondu dans la loi normal, donc on peut utiliser μ partout !! )
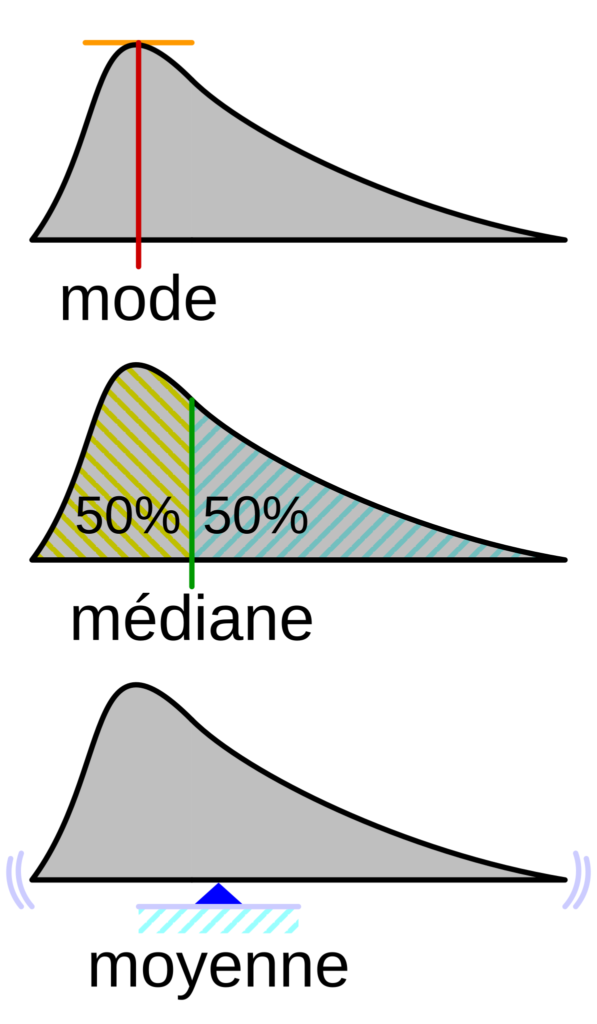
le mode → La valeur la plus représentée, la plus courante dans une population. Si la distribution est une loi normale, c’est le pic, le sommet de la courbe de Gauss. Si la distribution est multimodale, il peut y avoir plusieurs pics.
La médiane → la valeur centrale des valeurs possible, conçue pour avoir autant de valeurs plus petites que de valeurs plus grandes. On mentionne souvent le salaire médian, c’est à dire qu’il y a autant de gens qui gagnent moins que de gens qui gagnant plus. Ça a plus de sens que la moyenne arithmétique largement faussée par les valeurs extrême des revenus d’une poignée de milliardaires.
Loi normale → Aussi Courbe de Gauss. C’est la courbe en cloche qu’on obtient quand on observe une population de valeurs. C’est la distribution de valeur qu’on retrouve le plus couramment (comme pour le QI ou la distribution de billes qui tombent)
L’espérance → C’est la valeur attendue d’une distribution. Par exemple pour un grand nombre de jet de dé à 6 faces, on s’attend a avoir une moyenne global de 3,5 = (1+2+3+4+5+6)/6
échantillon → Un ensemble d’individus représentatif d’une population que l’on veut étudier. (ce qui évite d’avoir a mesurer des milliards d’individus alors qu’une partie seulement suffit !)
Distribution → est un tableau de données statistiques qui représente la valeur obtenue et la fréquence de l’apparition de la valeur. Si on classe ces données sous forme graphique on observe souvent la fameuse courbe en cloche étudiée par Gauss qu’on nomme la loi normale. Dans ce cas on a une distribution avec une valeur centrale. Il existe d’autres distributions de valeur courantes (ex: distribution de poisson, loi de Zipf, distribution binomiale, loi de pareto, etc..) ou carrément une distribution inconnue.
Quantile → Les quantiles sont les valeurs qui divisent un jeu de données en intervalles de même probabilités. C’est la généralisation du principe vu avec la médiane qui est la valeur qui coupe le jeu de données en deux. (Il existe d’autres division courantes, comme les quartiles, ou les centiles (= percentil en anglais))
Quartile → Les quartiles sont les 3 valeurs qui divisent le jeu de données en 4 parties de probabilité égale. (même nombre de valeur dans chaque groupe)
σ (sigma) → écart type (standard deviation en anglais d’où le fait que parfois indiqué S, dans des formules): σ = √variance
Variance: mesure la dispersion des valeurs d’un échantillon.

Distribution statistique

Si l’on mesure un phénomène, que l’on note la valeur obtenue, mais également le nombre de fois que cette valeur est apparue (la fréquence) on obtient une distribution statistique. La distribution la plus connue est la fameuse courbe de Gauss, aussi nommée loi normale.

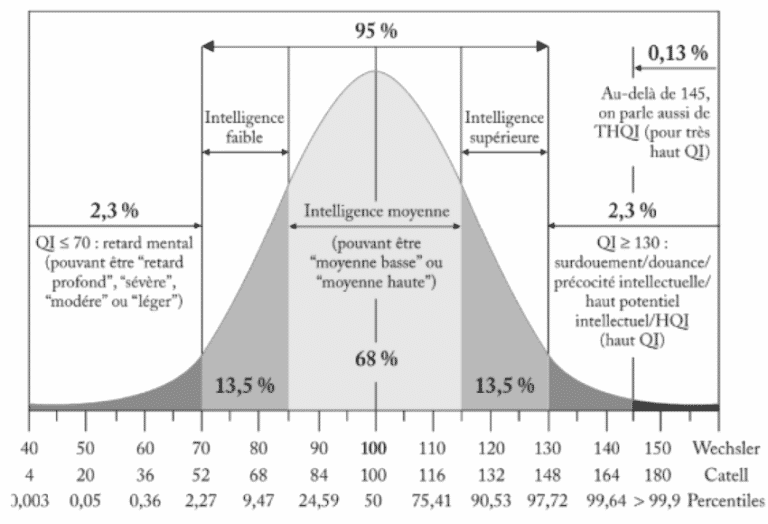
Distribution normale du Quotien Intellectuel

Le QI est basé sur une médiane à 100 sur une loi normale. On considère que l’intelligence « normale » ou « moyenne » c’est 15 points au dessus ou au dessous. Ainsi on retrouve 68% de la population. Un surdoué (ou HP) devrait être au dessus de 130 de QI.

Il existe des répartitions par pays des QI. Ce qui relance le fait de savoir si le QI est héréditaire ou non… Certains disent que le QI est génétique pour 50%, mais dépend des catégories sociales. Une étude norvégienne observe que si l’on prolonge d’une année la scolarité, on augmente le QI.

Après il faut relativiser, il y a différentes échelles suivant les tests. Il existe aussi d’autres forme d’intelligence que le QI. Notamment la théorie des intelligences multiples. (9 formes) selon Howard Garner. On en a déjà parlé en début d’année…

Un bon exemple pour montrer que le QI ne fait pas tout, c’est l’exemple des dirigeants Nazi. Lors du procès de Nuremberg, les 21 dirigeants Nazi accusés (et présents) ont passé un test de QI. Ce qui permettait de leur attribuer la responsabilité de leur actes. Il se trouve que la moyenne était de 128 !! le plus faibles des QI était de 106.

Construction d’une courbe de Gauss

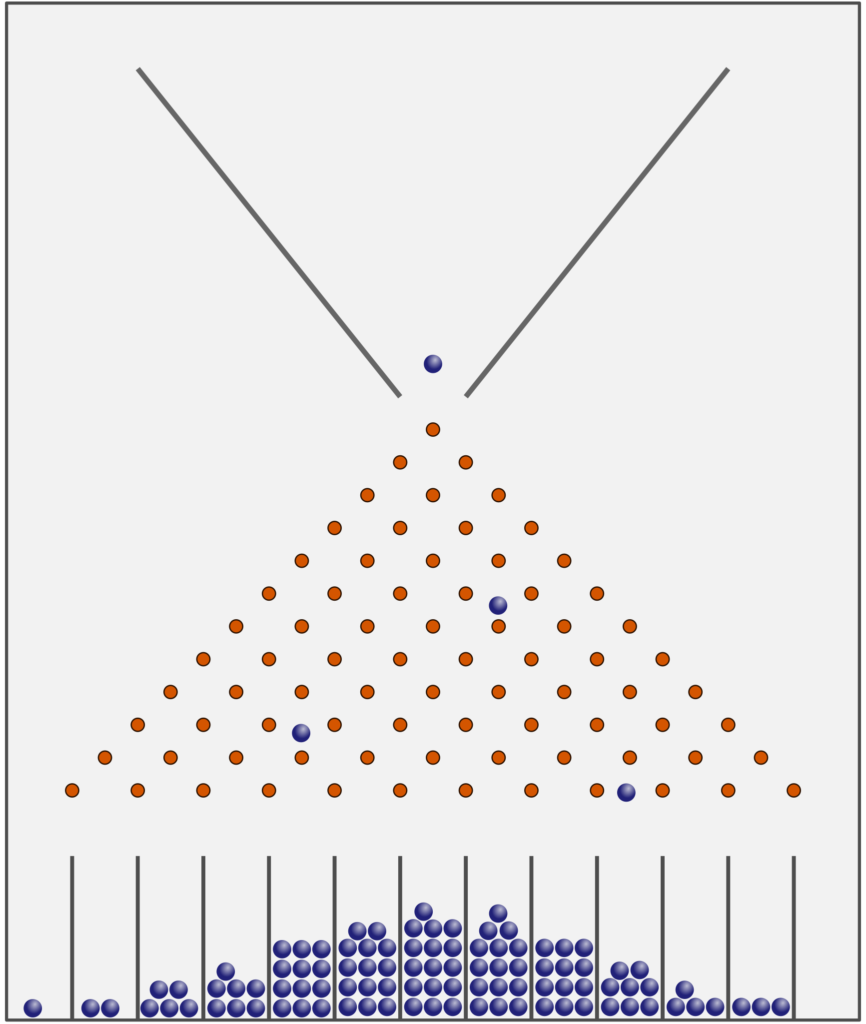
On peut observe la construction d’une courbe de Gauss en observant des billes tomber dans sur une planche de Galton.

On a des billes dans un entonnoir, et des clous sur une planche. A chaque fois qu’une bille touche un clou, elle a une chance sur 2 de passer à droite ou à gauche. (on a donc une distribution en loi binomiale si on a que 1 clou )

En ajoutant des rangées de clou, on va multiplier les choix binaires et ainsi faire converger la loi binomiale binaire en loi normale (courbe de Gauss).

Voici une simulation informatique de la planche de Galton dans laquelle on peut faire varier les paramètres….

Voici une courbe de Gauss sur geogebra avec laquelle on peut jouer sur les paramètres…

Exercice d’intuition sur la distribution des richesses

Imaginez une société idéale. Quelle devrait être la distribution des richesses ?

C’est l’expérience qui a été menée aux USA en posant la question à 5000 personnes….

Étude d’une distribution statistiques

Pour qualifier une distribution statistique on va étudier un certain nombre de ses paramètre. Ce qui va nous permettre de différentier une certaine distribution d’une autre, même si la forme globale est identique.

C’est ici que l’on va étudier les valeurs comme le mode, la moyenne, la médiane, la variance, l’écart-type.

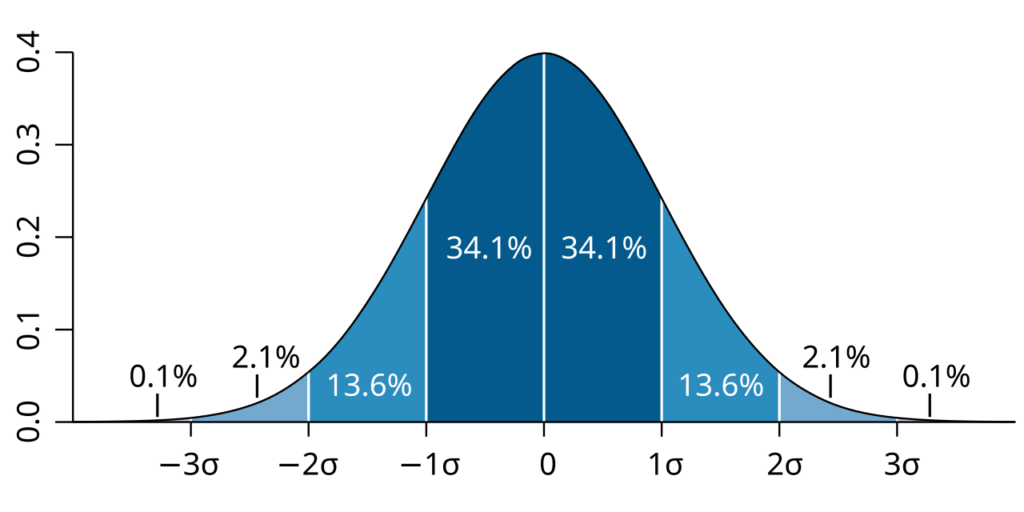
Voici une loi normale divisée en tranche de largeur d’un écart-type.

La moyenne

Il y a plusieurs façon de faire trouver une valeur moyenne.

La plus courante est la moyenne arithmétique. C’est somme des valeurs divisée par le nombre de valeurs.

C’est ce que vous avez l’habitude de pratiquer avec les moyennes de notes à l’école !

Petite subtilité, c’est si le nombre de valeur est déjà triée par fréquences.
C’est le cas avec l’exemple dans la vidéo ci-dessous qui utilise le nombre de buts par match durant la coupe du monde de foot 2010.

nombre de buts x_i	0	1	2	3	4	5	6	7
Nombre de matchs n_i	7	17	13	14	8	6	0	1

On a ici une moyenne pondérée. On multiplie chaque valeur par le nombre d’occurrence. (ce qui revient à une liste non triée où on a chaque valeur indépendante.)

La médiane

La médiane est une autre sorte de « moyenne ». On sépare le groupe de valeurs en deux. La médiane c’est qu’au moins la moitié des valeurs est à la valeurs de la médiane.

Il y a deux méthodes pour calculer la médiane d’une liste de valeurs.

Si le nombre de valeurs dans la liste est impair, c’est la valeur centrale.
Si le nombre de valeurs dans la liste est pair, c’est la moyenne des deux valeurs centrales.

Quel est donc le salaire médian en Suisse ?
Donc au moins la moitié des Suisses on un salaire du niveau du salaire médian.

On peut aussi voir les distributions des salaires pour différents métiers selon les offres d’emplois observées.

Un outil de cartographie statistiques pour lequel j’ai du bien réfléchir à la médiane….

  /**
  * Retourne la valeur médiane d'une liste de nombres indiqués dans un tableau.
  *
  * Utilisé pour le calcul de l'échelle automatique.
  * @return int la valeur médiane
  * @param a array de données numériques. ex: [5, 1, 1, 1, 5] => retourne : 1
  */
  function getMedianValue(a) {
    a = a.slice(0).sort(function(x, y) {
      return x - y;
    });
    var b = (a.length + 1) / 2;
    return (a.length % 2) ? a[b - 1] : (a[b - 1.5] + a[b - 0.5]) / 2;
}

Si on a une liste de fréquence de valeur, le calcul de la médiane se complique !! … Voici un exemple en vidéo avec les matchs de la coupe du monde de foot 2010 réparti dans un tableau en fonction du nombre de but par match.

Dans cet exemple, la médiane vaut 2 buts.

Ça signifie qu’il y a autant de match qui ont eu plus de deux but que de match qui ont eu moins de deux buts durant cette coupe du monde.

La variance et l’écart type

La variance mesure la dispersion des valeurs d’un échantillon.
L’écart type est la racine carrée de la variance.

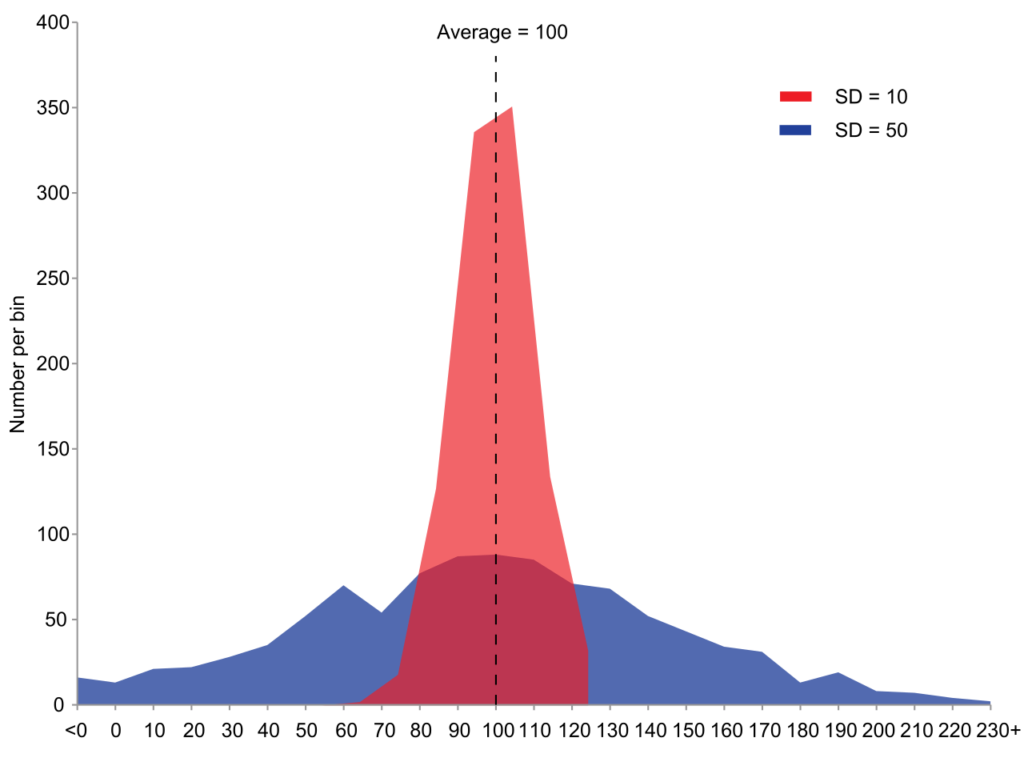
On a deux populations de données, avec chacune une courbe de Gauss centrée sur une moyenne de 100.

A l’oeil on voit bien que la distribution n’est pas du tout la même. Comment décrire la différence ?

On va utilise la variance. Si comme ici on connait la moyenne ${\bar {x}}$ , la variance est la moyenne des carrés des écarts à cette moyenne.

\[ V = \frac{1}{n}\sum_{i=1}^n \left(x_i – \overline{x}\right)^2 \]

(Autrement dit la variance est la différence entre la moyenne des carrés et le carré de la moyenne.)

Au delà de ces formules mathématiques pour geek des maths. C’est en fait pas très compliqué. Pour chaque valeur du tableau x_i , on va calculer la différence entre la valeur x et la moyenne ${\bar {x}}$ . On met tout ça au carré.
Puis on pondère en multipliant par la fréquence n_i de cette valeur. Une fois toutes les valeurs du tableau ajoutées. On va diviser tout ça par la somme des fréquences n. (en gros le nombre de valeurs totales de ma population.)

Ça me donne une formule du genre pour la variance:

\[ V = \frac{n_1*{ \left(x_1 – \overline{x}\right)^2} + n_2*{ \left(x_2 – \overline{x}\right)^2}+…+n_k*{ \left(x_k – \overline{x}\right)^2} }{n_1 + n_2 + … + n_k} \]

Donc l’écart-type nous donne:

\[ σ^2 = V \]

\[ σ = √V \]

Voici un exemple de calcul en vidéo à l’aide des buts de matchs de foot de la coupe du monde 2010.

Exercice de la vidéo pour calculer la variance et l’écart-type

Voici le fichier pour bidouiller …

Exercice stat match foot moyenne-variance-ecart-type Télécharger

Les vidéos sont tirées d’une playlist d’une série de vidéos qui explique les base de la statistique.

Statistique en classe Télécharger

Diagramme a barre et pour cent déTélécharger

Diagramme a barre Vélo électrique Télécharger

Suite de nombres M M E Q EIC V E-T Télécharger

Adaptation d’une population à son milieu

Voici un extrait d’une conférence à 1h00 qui nous parle de l’évolution darwinienne, de l’adaptation d’une population à son milieu.

On peut représenter l’adaptation d’une population à son milieu par une courbe de Gauss. Si l’écart type est faible, c’est que la population est super adaptée.

Quand l’environnement change, quelle est la partie qui dégage ? Le centre ou la périphérie….

…. réponse dans la vidéo !

…. indice pour la réponse: comment un dromadaire devient un chameau !

Quantiles

Les quantiles sont les valeurs qui divisent un jeu de données en intervalles de même probabilités. On a autant de chances de tomber dans un groupe ou un autre.

C’est la généralisation du principe vu avec la médiane qui est la valeur qui coupe le jeu de données en deux. (autant de chance de tombe au dessous qu’au dessus de la médiane)

Il existe d’autres divisions courantes, comme:

les quartiles → Les 3 valeurs qui divisent le jeu de données en 4 parties de probabilité égale. (même nombre de valeur dans chacun des 4 groupes)
les centiles (= percentil en anglais) → comme vu dans la vidéo ci dessus avec le 1% des personnes les plus riches des USA

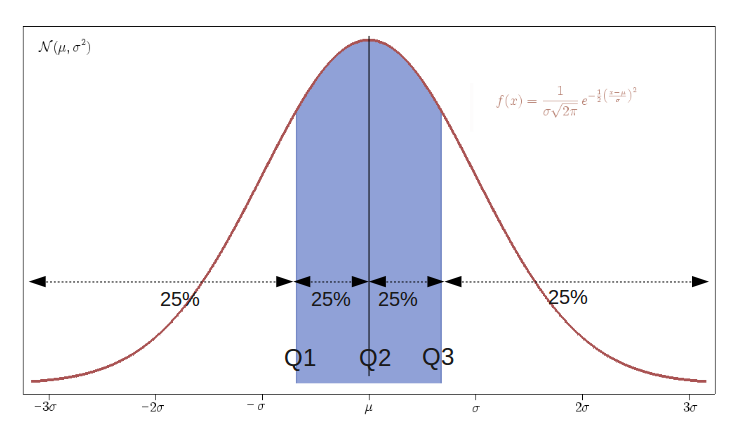
Densité de probabilité d’une loi normale de moyenne μ et d’écart-type σ.
On montre ici les trois quartiles Q₁, Q₂, Q₃.
L’aire sous la courbe rouge est la même dans les intervalles (−∞,Q₁), (Q₁,Q₂), (Q₂,Q₃), et (Q₃,+∞).
La probabilité d’être dans chacun de ces intervalles est de 25%.

Boite à moustache

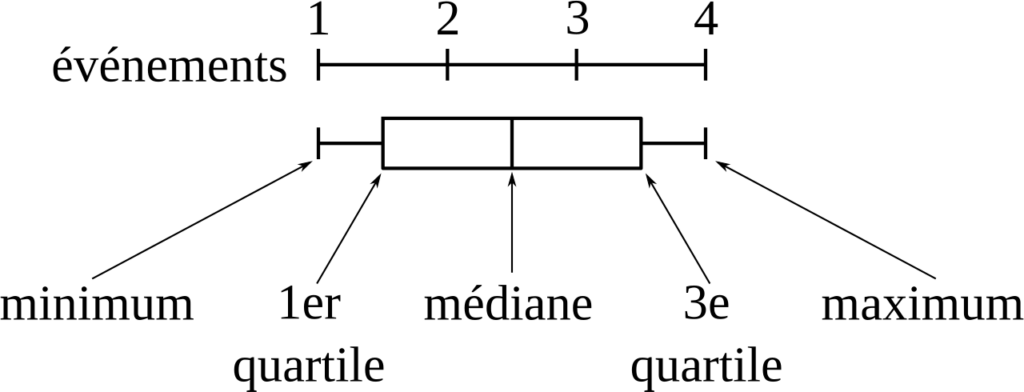
La boite à moustache, aussi appelée box plot est une représentation graphique de statistiques.

La boite à moustache indique directement les informations statistiques de bases d’une distribution: médiane, quartiles, minimum, maximum ou déciles.

IQR = Inter Quartile Range = écart interquartile → C’est est une mesure de dispersion qui vaut la différence entre le troisième et le premier quartile: IQR = Q3 – Q1.

La boite à moustache permet donc de comparer plusieurs distributions de données. Par exemple pour plusieurs sessions d’expériences.

Mesure de la vitesse de la lumière dans plusieurs session de l’expérience de Michelson et Morley

Voici comment créer des boites à moustaches avec excel.

Corrélation et causalité

Corrélation n’est pas causalité !
Quoique…. 😉

Corrélation entre le nombre de prix Nobel par pays et la consommation annuelle de chocolat par la population des pays concernés.

Le coefficient r correspond à la « qualité » de cette corrélation. Compris entre -1 et 1, plus la valeur absolue de r est proche de 1 plus la corrélation est forte (les points sont très proches d’une même droite qui passerait au centre de ce nuage de drapeau).

P indique une pente de cette droite non tracée par l’auteur significativement différente de 0.

Pour le détail voir la publication de Franz H. Messerli, 2012.

Ce genre de corrélation est très douteuse ! Attention à ne pas tomber dans les pièges !

C’est toujours tentant à partir d’un nuage données, d’en faire une « régression linéaire » pour en déterminer une loi générale.

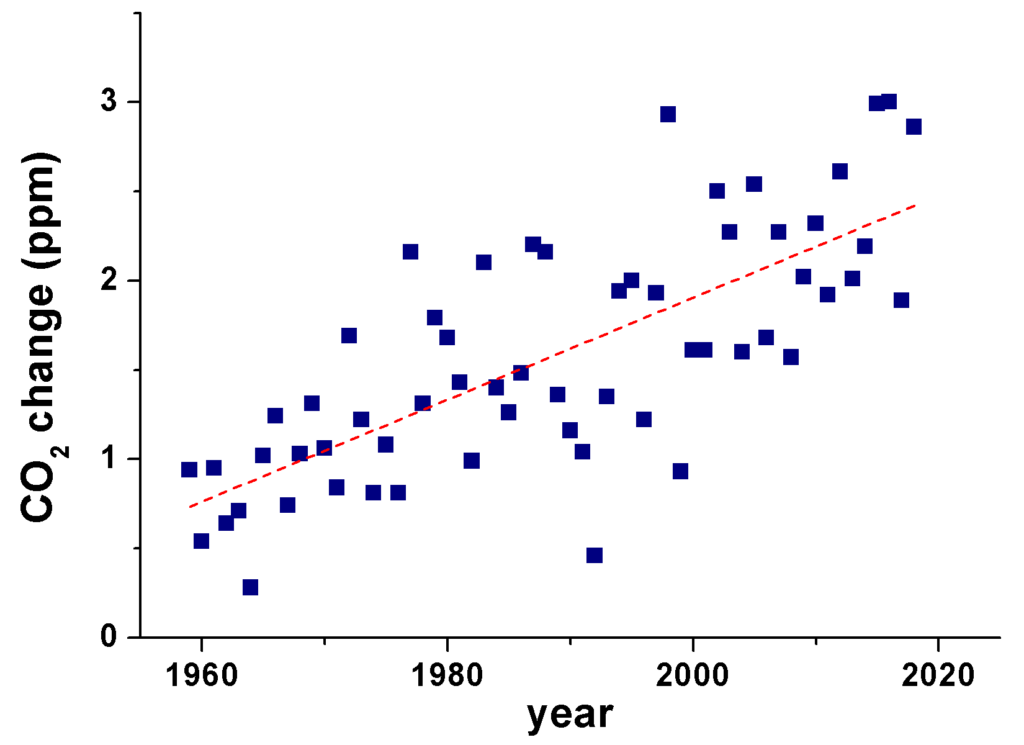
Voici un exemple de régression qui indique l’augmentation de CO2 dans l’atmosphère. Sans indication de la droite de régression, le graphe est dure à lire.

Augmentation annuelle du CO2 dans l’atmosphère

Voici la source des données texte qui ont permis de faire ce graphe. Ce sont les données de l’observatoire de Mauna Loa à Hawaï.

Le problème de l’échantillon

Si on prend un échantillon de population qui n’est pas représentatif on risque de ne pas avoir le bon résultat.

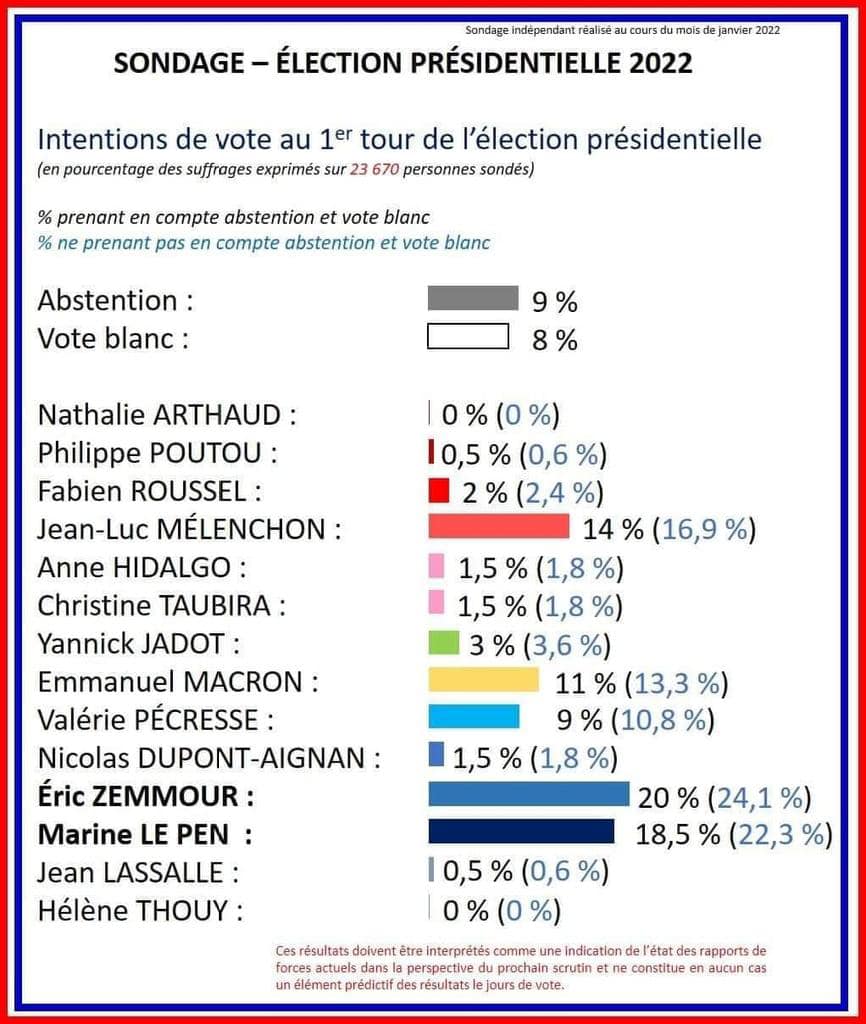
Voici les résultats de l’élection présidentielle de 2022 en France. C’est pas tout à fait ce que montre le sondage.

Les instituts de sondage tentent de créer des panels personnes représentatives d’une population, en âge, en sexe, en statut socio-économique, en localisation.

70 – Physique mécanique

70 physique mécanique – cours eit – exercice

En 1687 Newton publie son livre Philosophiae naturalis principia mathematica, et pose les bases de la physique mécanique toujours utilisée de nos jours en première approximation.

Newton a publié sa théorie de la gravitation, ainsi que les 3 lois de Newton:

le Principe d’inertie → En bref, tout corps au repos qui ne subit aucune influence extérieur continue à faire ce qu’il fait.
le Principe fondamental de la dynamique. → F = m*a. → L’accélération d’un corps est proportionnel aux forces qu’il subit et inversement proportionnel à sa masse. a = F/m
Le Principe d’action – réaction → Pour chaque force appliquée, il y a la même opposée.

Grandeurs et unités

Voici la formule de base à retenir pour tout ce qui est mouvement d’un corps.

\[ \vec{\mathrm{F}} = m \vec{a} \]

Il y a quelques grandeurs physiques à préciser:

F → La force exprimée en Newton [N]
m → La masse exprimée en Kilogramme [Kg]
a → L’accélération exprimée en mètre par seconde [m/s²]

Quand il y a une flèche sur la lettre qui représente la grandeur, c’est qu’on a une grandeur vectorielle. Ce n’est pas juste un nombre, mais la grandeur a aussi une direction.

Première loi de Newton : principe d’inertie

Seconde loi de Newton

Permet de prévoir la trajectoire d’un objet.

\[ \vec{\mathrm{F}} = m \vec{a} \]

3ème loi de Newton: action – réaction

C’est ainsi qu’un fusée peut avancer à propulser de la masse très vite derrière elle.

Gravitation

Satellite

Énergie

L’énergie c’est la capacité à transformer son environnement.
L’énergie c’est la monnaie de l’univers.

L’énergie se présente sous de nombreuses forme:

Le premier principe de la thermodynamique est le principe de la conservation de l’énergie. → L’énergie se transforme, mais ne se perd pas.

Le second principe de la thermodynamique indique que le rendement de la transformation n’est pas optimal. Chaque transformation d’énergie induit une « perte » d’énergie en qualité, l’augmentation du désordre: l’entropie.
(par exemple, le pétrole est une source d’énergie d’une grande qualité, très facilement utilisable. Mais en l’utilisant comme source d’énergie mécanique, dans une voiture par exemple, une bonne partie de l’énergie se transforme en bruit et en chaleur, des formes d’énergie très peu utilisable.)

Énergie potentielle de pesenteur

L’Énergie potentielle est une énergie qu’un objet emmagasine par le simple fait d’être dans le champ de gravité de la Terre.

\[ \mathrm{E} = m g h \]

E → énergie en joule [J]
m → masse en [Kg]
g → accélération de la gravité terrestre = 9,81 m/s²
h → hauteur en mètre [m]

Plus haut on a utilisé F = m*a, donc avec une accélération a. Ici on a une accélération particulière, celle de la gravité terrestre qui vaut à la latitude de 45° 9,81 m/s².

Le principe d’équivalence déterminé par Einstein montre qu’on peut considérer de façon identique l’accélération d’un champ gravitationnel et l’accélération mécanique. (dans une voiture par exemple)

Donc on peut calculer issue du champ gravitationnel de la Terre sur un objet. On reprend la formule: F = m*a qu’on transforme en F = m*g

On a donc ici une force que l’on appelle le poids.

Ainsi, avec une masse identique, on peut avoir un poids différents suivant sur quelle planète on se trouve.

Lune → g = 1,622 m/s²

Énergie cinétique

L’Énergie cinétique est l’énergie emmagasinée par un objet en mouvement.

\[ \mathrm E_c \approx \frac{1}{2} m v^2 \]

100 – Optique

Loi de Snell Descartes